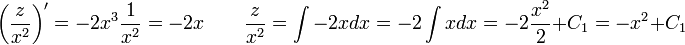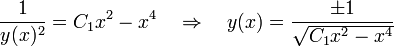Ecuaciones de Bernoulli
es una ecuación diferencial ordinaria de primer orden, formulada por Jacob Bernoulli. Esta ecuación fue transformada, por Gottfried Leibniz en 1693 y por Johann Bernoulli en 1697, en una ecuación diferencial lineal de primer orden, mediante la sustitución y1-α = v,1 que se caracteriza por adoptar la forma:
{dy}+P(x)y=Q(x)y^ª{dx}
Algoritmo:
Si se descuentan los casos particulares en que α=0 y α=1 y se divide la ecuación por yα se obtiene:
Definiendo:
o,equivalentemente, Z = y1-α
lleva inmediatamente a las igualdades:
Gracias a esta última relación se puede reescribir como:
Donde

es una constante arbitraria. Pero como
Z =
y1-α se tiene que:
Finalmente, las funciones que satisfacen la ecuación diferencial pueden calcularse utilizando la expresión:
Con

. Donde el factor integrante se define en, por ejemplo, 0 < x < ∞
Caso particular: α = 0
En este caso la ecuación se reduce a una ecuación diferencial lineal cuya solución viene dada por:
Caso particular: α = 1
Tenemos una ecuación diferencial lineal (Ecuación de variables separables). En este caso la solución viene dada por:
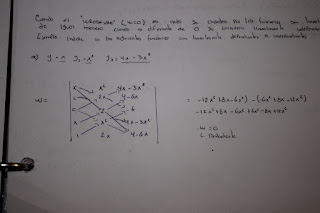
Ejemplo:
Para resolver la ecuación:
Multiplicando la ecuación anterior por el factor:
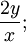
se llega a:
Si se sustituye en la última expresión y operando:
Que es una ecuación diferencial lineal que puede resolverse fácilmente. Primeramente se calcula el
factor integrante típico de la ecuación de Bernouilli:
Y se resuelve ahora la ecuación:
Deshaciendo ahora el cambio de variable:
Teniendo en cuenta que el cambio que hicimos fue
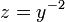
:







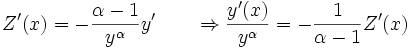

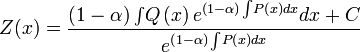
 es una constante arbitraria. Pero como Z = y1-α se tiene que:
es una constante arbitraria. Pero como Z = y1-α se tiene que:![{y^{(\alpha-1)}}={\frac {{e^{\left( 1-\alpha \right) \int \!P \left( x \right) {dx}}}}{ \left( 1-\alpha \right) \int \!Q \left( x \right){e^{
\left( 1-\alpha \right) \int \!P \left( x \right) {dx}}} {dx}+C}} \qquad \Rightarrow y(x)={\sqrt [\alpha-1]{\frac {{e^{-(\alpha-1)\int \!P \left( x \right) {dx}}}}{ \left( 1-\alpha \right) \int \!Q \left( x \right){e^{
\left( 1-\alpha \right) \int \!P \left( x \right) {dx}}} {dx}+C}}}](https://upload.wikimedia.org/math/b/0/6/b0683a1d7a3aa809bbc61389a1446b37.png)
![y(x)={\frac {{e^{-\int \!P \left( x \right) {dx}}}}{\sqrt [\alpha-1]{ \left( 1-\alpha \right) \int \!Q \left( x \right) {e^{
\left( 1-\alpha \right) \int \!P \left( x \right) {dx}}}{dx}+C}}}](https://upload.wikimedia.org/math/9/a/4/9a47238d1aa4d74ae68a27dd1f66ea05.png)
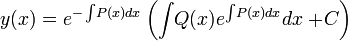
![\ln\ \!y(x) = \int [Q(x)-P(x)]dx + C](https://upload.wikimedia.org/math/2/1/e/21eb44df1817fad22985bcdfff9c4922.png)
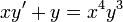
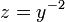

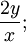 se llega a:
se llega a: