Ecuaciones Diferenciales Lineales
Son las que se encuentran de la siguiente forma
Algoritmo:
1. Se Identifica el factor integrante
2. Se multiplicar la ecuación diferencial por el factor integrante.
3. Se Sustituye en el primer miembro la derivada
d/dx Y*m
4. Se Integra la ecuación y se despeja la variable independiente.
Ejemplo:
Esta ecuación tendrá una solución en el intervalo 0 ≤ x ≤ 1 (para g(x) = 1) y otra en el resto (x > 1). Podemos poner entonces:
- y' + 2y = 1
Y tenemos una ecuación diferencial lineal no exacta de la que podemos calcular un factor integrante por:

Lo que nos da una solución general de la forma:

Y para el caso particular y(0) = 0

Podemos ver que esta última ecuación toma para x = 1 el valor:

Con lo que la siguiente parte se ha de resolver como:
Lo que nos da una solución general de la forma:
Y para el caso particular y(0) = 0
Podemos ver que esta última ecuación toma para x = 1 el valor:
Con lo que la siguiente parte se ha de resolver como:
- y' = 2y = 0
Con la condición dada por la ecuación anterior.
Tenemos entonces:

Pero teniendo en cuenta el valor de y(1):

Obtenemos como solución para el intervalo x > 1:

Tenemos entonces:
Pero teniendo en cuenta el valor de y(1):
Obtenemos como solución para el intervalo x > 1:
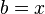




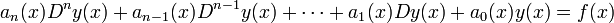
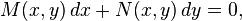
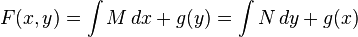
 con respecto a la variable independiente de g.
con respecto a la variable independiente de g.