Ecuación Diferencial Lineal
Estas ecuaciones tienen la propiedad de que el conjunto de las posibles soluciones tiene estructura de espacio vectorial de dimensión finita cosa que es de gran ayuda a la hora de encontrar dichas soluciones.
Algoritmo:
*Se identifica
*Se resuelve la ecuación.
*Al obtener la solución general despejamos C.
* sutituimosCen la solución general.
*Se hace el proceso de -3 al 3 con valores de X.
Ejemplo
Tenemos 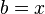 . Proponemos
. Proponemos  (polinomio de primer orden). Las constantes
(polinomio de primer orden). Las constantes  y
y  quedan determinadas tras aplicar los requerimientos de la ecuación a la solución particular (derivar n veces, multiplicar por
quedan determinadas tras aplicar los requerimientos de la ecuación a la solución particular (derivar n veces, multiplicar por  coeficientes constantes, etc.).
coeficientes constantes, etc.).
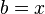 . Proponemos
. Proponemos  (polinomio de primer orden). Las constantes
(polinomio de primer orden). Las constantes  y
y  quedan determinadas tras aplicar los requerimientos de la ecuación a la solución particular (derivar n veces, multiplicar por
quedan determinadas tras aplicar los requerimientos de la ecuación a la solución particular (derivar n veces, multiplicar por  coeficientes constantes, etc.).
coeficientes constantes, etc.).Vemos que esta ecuación es de la forma:
Pero no es diferencial exacta. Calculamos el factor integrante aplicando la fórmula dada:
Y la solución general vendrá dada por:
Si queremos buscar el caso y(1) = 2, hacemos:
- 2 = 1 + C ; C = 1
Con lo que la solución de la ecuación será:

La representación gráfica de la solución da un haz de curvas como el adjunto.
La representación gráfica de la solución da un haz de curvas como el adjunto.
No hay comentarios.:
Publicar un comentario