Ecuaciones Diferenciales Lineales
Una ecuación diferencial lineal ordinaria es una ecuación diferencial que tiene la forma:
Para que una ecuación diferencial sea lineal debe darse que no aparezcan productos de la función incógnita consigo misma ni con ninguna de sus derivadas.
Algoritmo:
1. Identificar el factor integrante M=e^{P(x)dx
2. Multiplicar la ecuación diferencial por el factor integrante.
3. Sustituir en el primer miembro la derivada del producto de la función y el factor integral
d/dx Y*m
4. Integrar la ecuación y despejar la variable independiente. Ejemplo:
y+y-e^3x=0
y´+y=e^3x
p(x)=1
M=e^S1dx =e^x
M=e^x
e^xy+e^x y =e^3x*e^x
d/dx y* e^x =ye^x + e^xy´
Sd/dx y*e^x = 1/4 Se^4x dx
y*e^x=1/4e^4x+c
y=1/4e^4x+c/e^x
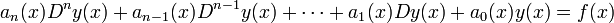
No hay comentarios.:
Publicar un comentario