Para resolver una ecuación diferencial de este tipo, se ha de seguir los siguientes pasos:
- Comprobar la exactitud de la ecuación, esto es, verificar si las derivadas parciales de M (con respecto a y) y de N (con respecto a x) son iguales.
- Se integra M o N a conveniencia (M respecto a x ó N respecto a y) obteniéndose de este modo la solución general de la ecuación aunque con una función incógnita g que aparece como constante de integración. Esto es:
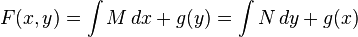
- Para despejar la función g se deriva
 con respecto a la variable independiente de g.
con respecto a la variable independiente de g.
- Se iguala g' con M o N (si se integró M se iguala a N y viceversa.), despejando y luego integrando con respecto a la variable independiente de g; de este modo se encontrará la función g.
- Finalmente se reemplaza el g encontrado en la solución general

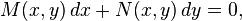
 con respecto a la variable independiente de g.
con respecto a la variable independiente de g.
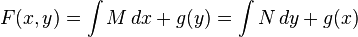
No hay comentarios.:
Publicar un comentario